正文
匹配滤波器是为了实现抽样判决器在抽样时刻得到最大信噪比,那如何实现这个最佳滤波器的传输函数呢?
匹配滤波器的传输函数
假设滤波器的传输函数是H(ω)。它的输入端是噪声和信号之和 x(t)=s(t)+n(t)。其中n(t)是白噪声,它的功率密度谱为Pn(ω)=n/2。s(t)的频谱假设为S(ω),由于信号与噪声互不相关,滤波器是线性网络。根据叠加原理,可以对两者通过滤波器的情况分别讨论,它的输出肯定是两个部分的和y(t)=So(t)+No(t)。其中有用信号为1/2π乘上H(ω)S(ω)*exp(jωt)中ω在负无穷到正无穷的积分,而输出噪声的平均功率为:
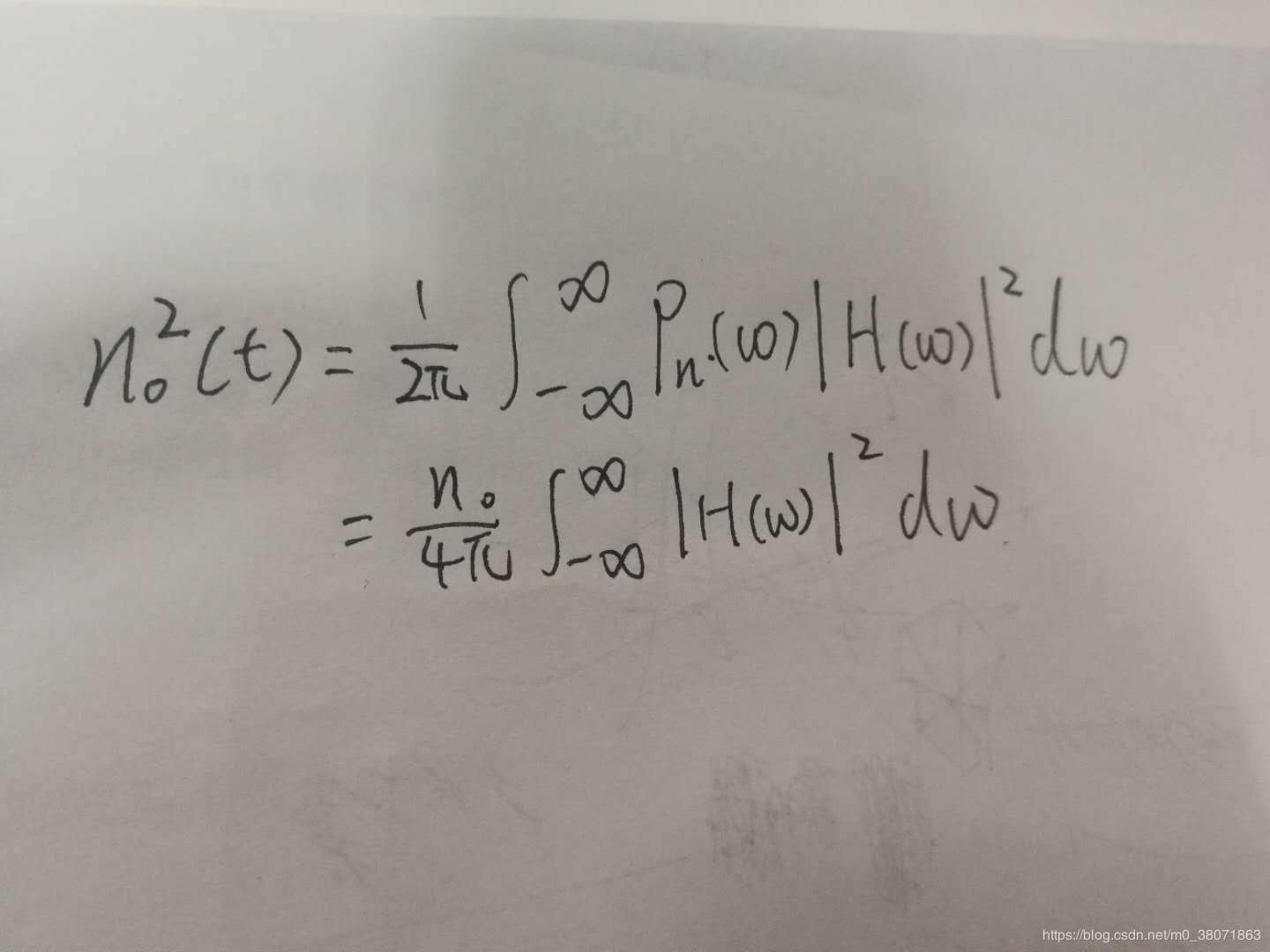
令to为某一抽样时刻,定义滤波器在to时刻输出的有用信号瞬时功率和噪声平均功率之比为: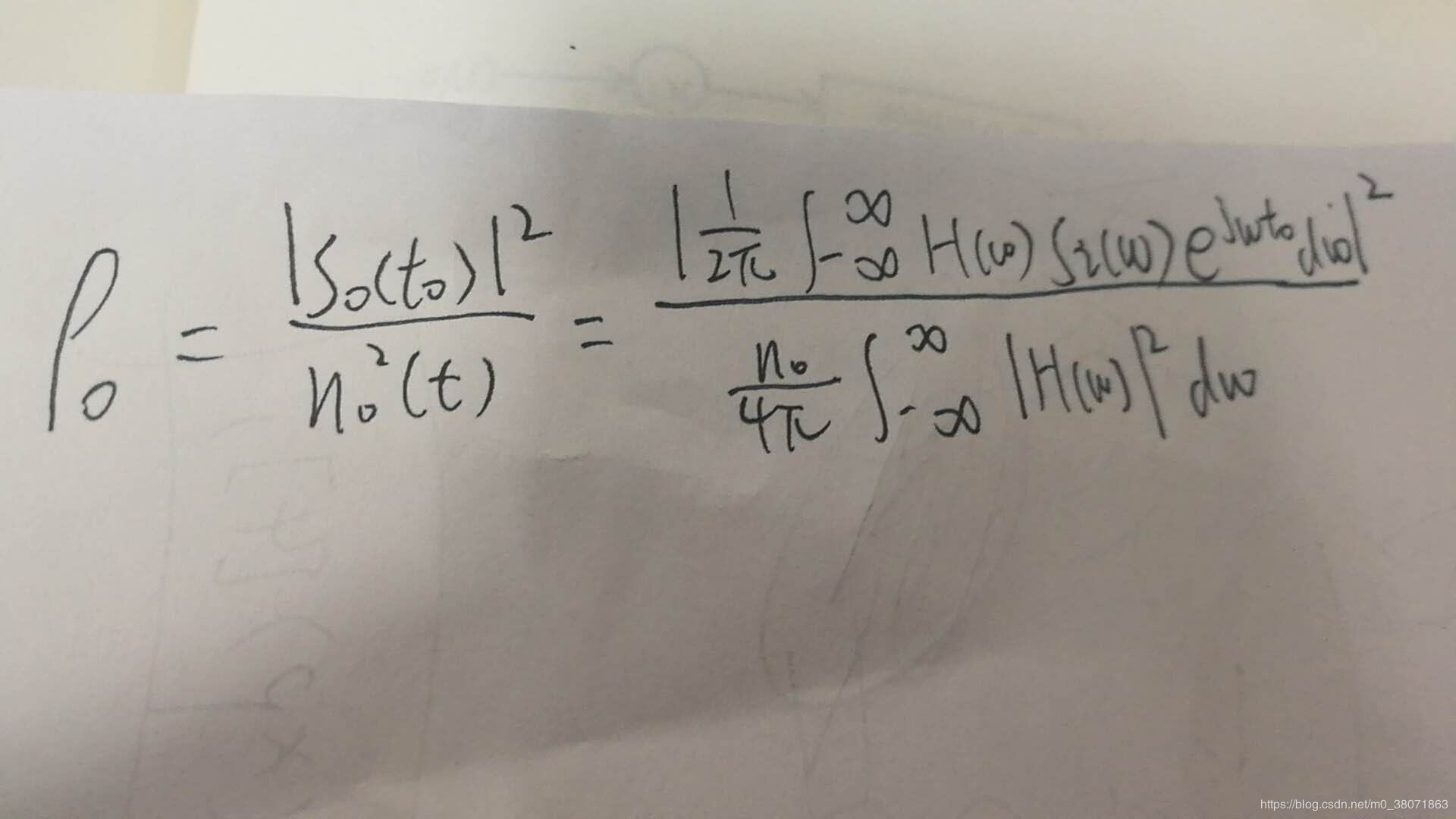
根据施瓦茨不等式,若要让此等式的比值最大,令F1(ω)=H(ω),F2(ω)=S(ω)exp(jωt),只有在F1(ω)=kF1(ω)的情况下才成立,并且最大信噪比为2E/no。其中E为输入信号能量。所以当H(ω)=kS(ω)exp(jωt)时,可以输出最大信噪比,因为它只与输入信号有关,所以叫做匹配滤波器。